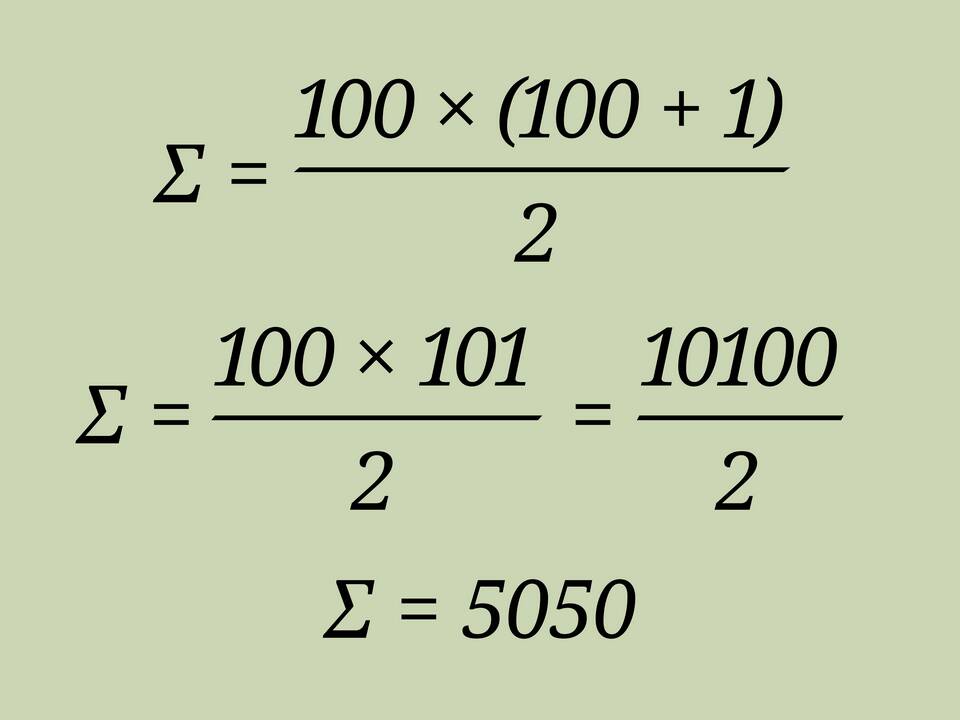Сумма чисел от 1 до 20 - это классическая математическая задача, которая демонстрирует применение различных методов суммирования. Рассмотрим несколько способов ее решения.
Содержание
Прямое суммирование
Самый простой способ - последовательное сложение всех чисел от 1 до 20:
| 1 + 2 | = 3 |
| 3 + 3 | = 6 |
| 6 + 4 | = 10 |
| ... | ... |
| 190 + 20 | = 210 |
Формула Гаусса
Более эффективный метод - использование формулы суммы арифметической прогрессии:
- Формула: S = n(n+1)/2
- Где n = 20
- Расчет: S = 20×21/2 = 210
Разбиение на пары
Метод, который использовал юный Гаусс:
| 1 + 20 | = 21 |
| 2 + 19 | = 21 |
| 3 + 18 | = 21 |
| ... | ... |
| 10 пар × 21 | = 210 |
Проверка другими методами
Сумма через квадраты
Используя формулу суммы квадратов:
- Σn² = n(n+1)(2n+1)/6 = 2870
- Σn = √(Σn² - Σ(n²-n)) ≈ 210
Математическая индукция
- База: для n=1: 1 = 1×2/2 - верно
- Предположение: для n=k сумма равна k(k+1)/2
- Шаг: для n=k+1 сумма S = k(k+1)/2 + (k+1) = (k+1)(k+2)/2
Практическое применение
| В статистике | Расчет средних значений |
| В программировании | Оптимизация циклов |
| В экономике | Расчет совокупных показателей |
Таким образом, сумма всех натуральных чисел от 1 до 20 равна 210. Это значение можно получить различными методами, каждый из которых подтверждает правильность результата.