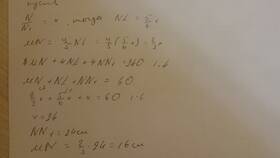Доверительный интервал - это диапазон значений, который с определенной вероятностью содержит неизвестный параметр генеральной совокупности. Рассмотрим методы его расчета для различных статистических задач.
Содержание
Основные понятия
- Доверительная вероятность (уровень доверия) - обычно 90%, 95% или 99%
- Точечная оценка - среднее значение выборки
- Предельная ошибка - полуширина интервала
- Объем выборки - количество наблюдений
Формула доверительного интервала
Доверительный интервал = Точечная оценка ± (Критическое значение × Стандартная ошибка)
Пошаговый алгоритм расчета
Определение параметров
- Выберите уровень доверия (1-α)
- Рассчитайте среднее значение выборки (x̄)
- Определите стандартное отклонение (σ или s)
- Установите объем выборки (n)
Выбор типа интервала
| Тип данных | Формула |
| Для среднего при известном σ | x̄ ± zα/2 × (σ/√n) |
| Для среднего при неизвестном σ | x̄ ± tα/2 × (s/√n) |
| Для доли | p̂ ± zα/2 × √(p̂(1-p̂)/n) |
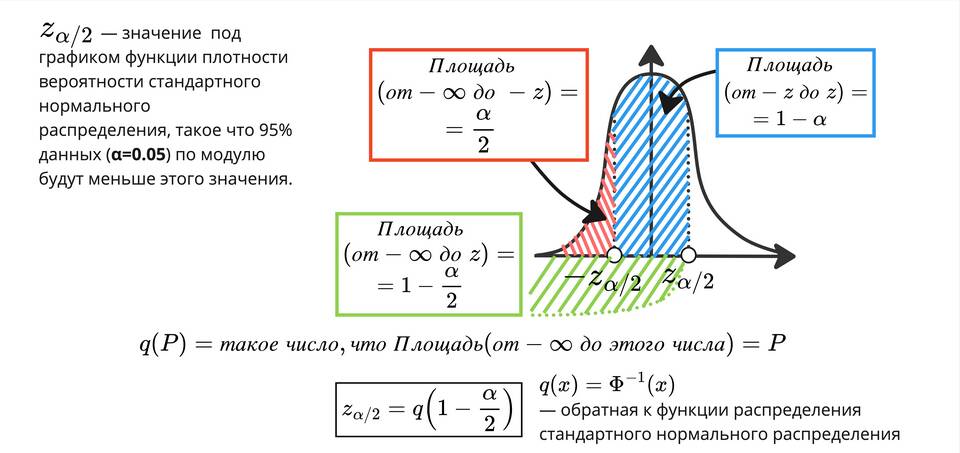
Расчет критических значений
- z-значения для нормального распределения
- t-значения Стьюдента для малых выборок
- Использование статистических таблиц
Пример расчета для среднего
- Дано: x̄ = 50, s = 10, n = 30, доверительный уровень 95%
- Находим t-критерий для α/2 = 0.025 и df = 29: ≈2.045
- Стандартная ошибка = 10/√30 ≈ 1.826
- Предельная ошибка = 2.045 × 1.826 ≈ 3.735
- Доверительный интервал: 50 ± 3.735 → [46.265; 53.735]
Факторы, влияющие на ширину интервала
| Фактор | Влияние на ширину |
| Уровень доверия | Чем выше - тем шире |
| Размер выборки | Чем больше - тем уже |
| Разброс данных | Чем больше - тем шире |
Практическое применение
- Определение точности оценок
- Сравнение групп
- Проверка статистических гипотез
- Прогнозирование
Программные средства
- Excel: функции ДОВЕРИТ.НОРМ() и ДОВЕРИТ.СТЬЮДЕНТ()
- R: t.test(), prop.test()
- Python: scipy.stats.t.interval()
- SPSS: Analyze → Descriptive Statistics → Explore
Ошибки при построении
- Использование z-распределения для малых выборок
- Неучет типа распределения данных
- Некорректный расчет стандартной ошибки
- Интерпретация как вероятности для параметра
Построение доверительного интервала - важный статистический метод, позволяющий оценить точность полученных результатов. Правильное применение соответствующих формул обеспечивает надежность выводов в исследованиях.